LA FUNCIÓN LINEAL DE COSTO
lunes, 8 de octubre de 2018
domingo, 17 de abril de 2016
QUE ES UN MANUAL:
Una ecuación es una igualdad entre dos expresiones algebraicas, denominadas miembros, en las que aparecen valores conocidos o datos, y desconocidos o incógnitas, relacionados mediante operaciones matemáticas.
RELACIONES ENTRE GEOMETRÍA Y ECUACIONES:
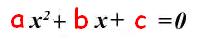
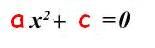 En
el segundo caso, falta el término independiente, o sea el que contiene el
coeficiente llamado “c”, por lo que la forma tipo quedará ahora así:
En
el segundo caso, falta el término independiente, o sea el que contiene el
coeficiente llamado “c”, por lo que la forma tipo quedará ahora así:
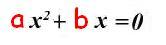
Se
denomina manual a toda guía de instrucciones que sirve para el uso de un
dispositivo, la corrección de problemas o el establecimiento de procedimientos
de trabajo. Los manuales son de enorme relevancia a la hora de transmitir
información que sirva a las personas a desenvolverse en una situación
determinada. En general los manuales son frecuentes acompañando a un
determinado producto que se ofrece al mercado, como una forma de soporte al
cliente que lo adquiere. En este caso, el manual suele tener una descripción
del producto y de la utilización que del mismo debe hacerse, ya sea para
obtener un buen rendimiento de éste como para dar cuenta de posibles problemas
y la forma de evitarlos.
TIPOS DE MANUALES
Política: sin ser formalmente reglas en este manual se determinan y regulan la actuación y dirección de una empresa en particular.
Procedimientos: este manual determina cada uno de los pasos que deben realizarse para emprender alguna actividad de manera correcta.
Técnicas: estos manuales explican minuciosamente como deben realizarse tareas particulares, tal como lo indica su nombre, da cuenta de las técnicas.
Bienvenida: su función es introducir brevemente la historia de la empresa, desde su origen, hasta la actualidad. Incluyen sus objetivos y la visión particular de la empresa. Es costumbre adjuntar en estos manuales un duplicado del reglamento interno para poder acceder a los derechos y obligaciones en el ámbito laboral.
Puesto: determinan específicamente cuales son las características y responsabilidades a las que se acceden en un puesto preciso.
Múltiple: estos manuales están diseñados para exponer distintas cuestiones, como por ejemplo normas de la empresa, más bien generales o explicar la organización de la empresa, siempre expresándose en forma clara.
Finanzas: tiene como finalidad verificar la administración de todos los bienes que pertenecen a la empresa. Esta responsabilidad está a cargo del tesorero y el controlador.
Finanzas: tiene como finalidad verificar la administración de todos los bienes que pertenecen a la empresa. Esta responsabilidad está a cargo del tesorero y el controlador.
Sistema: debe ser producido en el momento que se va desarrollando el sistema. Está conformado por otro grupo de manuales.
CUAL VOY A USAR
EL MANUAL QUE YO VOY A USAR ES EL DE MÚLTIPLE PORQUE ME PARECE UNA FORMA MAS FÁCIL DE EXPONER LAS FORMAS MAS FÁCIL METE Y CLARAS
QUE SON ECUACIONES:
Una ecuación es una igualdad entre dos expresiones algebraicas, denominadas miembros, en las que aparecen valores conocidos o datos, y desconocidos o incógnitas, relacionados mediante operaciones matemáticas.
RELACIONES ENTRE GEOMETRÍA Y ECUACIONES:
la acepción geométrica del producto notable del cuadrado
de la suma de dos cantidades en relación a la noción de área, tomando en consideración la
aditividad que guardan las figuras geométricas elementales que la conforman al construir este
producto notable en forma geométrica, bien sean estos paralelogramos unos cuadrados o
rectángulos. Además, veremos la aplicación de esta suma del cuadrado de dos cantidades tratados
desde un punto de vista geométrico aplicado en la solución de la ecuación cuadrática o mejor
conocida ecuación de segundo grado, usando algunos procesos cognitivos y algunas aplicaciones
algebraicas.
CLASIFICACIÓN DE ECUACIONES DE SEGUNDO GRADO:
Ecuaciones
completas de segundo grado
Son aquellas que tienen un término de segundo grado (o sea
un término “en X 2 ” ), un término lineal (es decir “en x”) y un
término independiente, es decir un número sin x. Un ejemplo de una ecuación de
este tipo es la siguiente:
2x2 – 4x – 3 = 0
Ten en cuenta que al coeficiente del término cuadrado,
habitualmente se le llama a, al del término lineal se le llama b y al
independiente se le llama c, de modo que en este caso: a=2, b=-4 y c=-3 .
Por este motivo, la forma tipo de estas ecuaciones
se representa con la siguiente expresión general:
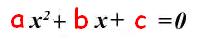
Ecuaciones
incompletas de segundo grado
Para hacerte bien sencillo el concepto, te digo que una
ecuación de segundo grado es incompleta cuando le falta uno de estos
tres términos que hemos mencionado que existen en las ecuaciones completas de
segundo grado; eso sí: está claro que el término cuadrado… ¡no puede faltar! de
lo contrario ésta no será una ecuación de segundo grado.
Pues bien entonces, hay dos tipos de ecuaciones
incompletas de segundo grado: aquellas a las que les falta el término
lineal (o sea el término “en x”) y aquellas a las que les falta el
término independiente (o sea el que no tiene x).
En el primer caso falta el término que contiene el
coeficiente llamado “b”, por lo que la forma tipo quedará así:
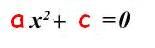 En
el segundo caso, falta el término independiente, o sea el que contiene el
coeficiente llamado “c”, por lo que la forma tipo quedará ahora así:
En
el segundo caso, falta el término independiente, o sea el que contiene el
coeficiente llamado “c”, por lo que la forma tipo quedará ahora así: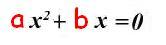
Resumiendo: las
ecuaciones de segundo grado se clasifican en completas e incompletas. Las
completas cuentan con tres términos cuyos coeficientes son a, b y c. Las
ecuaciones incompletas se dividen a su vez en dos tipos, según el falte el
término lineal o el término independiente.
EN QUE CARRERAS SE USA LAS ECUACIONES CUADRÁTICAS:
El ejército y el cumplimiento de la ley
Las ecuaciones cuadráticas se utilizan a para describir el movimiento de los objetos que vuelan por el aire. Si planeas unirte al ejército y trabajar con artillería y tanques, entonces vas a utilizar regularmente la ecuación cuadrática para predecir dónde aterrizarán los proyectiles. La policía también las utiliza para determinar las trayectorias de las balas y para averiguar la de los que han estado involucrados en accidentes.
Ingeniería
Los ingenieros de tipo utilizan estas ecuaciones. Son necesarias para el diseño de cualquier pieza de equipo que sea curva, como las carrocerías de los automóviles. Los ingenieros automotrices también las utilizan para diseñar los sistemas de frenos. Por razones similares, los ingenieros aeroespaciales trabajan con ellas regularmente. Los ingenieros eléctricos y químicos trabajan con muchos sistemas complejos que involucran ecuaciones cuadráticas. Lo mismo ocurre con los ingenieros informáticos. Los ingenieros de audio utilizan estas ecuaciones para diseñar sistemas de sonido que tengan la mejor calidad de sonido posible.
martes, 29 de marzo de 2016
INTRODUCCIÓN
EN ESTE BLOGGER HABLAREMOS SOBRE ALGUNOS EMPRESARIOS O TRABAJADORES QUE ESTUVIERON EN LA BIBLIA Y CUAL ES EL EMPLEO DE ELLOS Y COMO HACÍAN PARA SUSTENTAR A SU FAMILIA.
Y TAMBIÉN HABLAREMOS SOBRE LAS FUNCIONES LINEALES DE COSTO EXPLICAREMOS QUE QUE ES, HABRÁN ALGUNOS EJEMPLOS DE TALLERES O EJERCICIOS SOBRE EL TEMA DE FUNCIONES LINEALES DE COSTO
CONCLUSIONES
LAS CON CONCLUSIONES QUE PUDIMOS SACAR O CONCLUIR FUE DE QUE PUDIMOS APRENDER MAS SOBRE LA FUNCIÓN LINEAL DE COSTO Y HA SI SABER MAS SOBRE EL TEMA PORQUE ES IMPORTANTE SABER SOBRE ESTE TEMA POR QUE ES IMPORTANTE PARA LA VIDA DE UNA PERSONA
OTRAS CONCLUSIONES FUE QUE SOLO NO ENCONTRAMOS EMPRESARIOS DES DE HACE POCO TIEMPO SINO QUE TAMBIÉN EN EL TIEMPO DE JESÚS TAMBIÉN HABÍAN MUCHAS PERSONAS Y SEGUIDORES DE JESÚS QUE ERAN EMPRESARIOS Y QUE TAMBIÉN PORQUE NOSOTROS NO PODEMOS SER EMPRESARIOS
domingo, 13 de marzo de 2016
5 TEXTOS BÍBLICOS DONDE HABLEN SOBRE LAS EMPRESAS:
MATEO 13:55: ¿No es éste el hijo del carpintero? ¿No se llama su madre María, y sus hermanos Jacobo, José, Simón y Judas?
SAN MATEO: era un centro mercantil, residencia de mercaderes y traficantes, de tenderos y comisionistas, y, punto estratégico para los cambistas y los recaudadores, oficina importante de los publicanos de Galilea.
SAN LUCAS: Con educación griega fue un médico de Antioquía, pagano no judío, antes de convertirse al cristianismo. No conoció a Jesús.
SAN PEDRO: era un hombre cuyo trabajo era la pezca y los vendía en el mercado para poder ganar dinero
SAN PABLO: era un hombre cuyo trabajo era hacer tiendas de campaña para poder venderlas
CUANTOS EMPRESARIOS ENCONTRAMOS EN LA BIBLIA
1 JOSE: era carpintero y su tipo de trabajo o empresa era trabajar en carpintería para sustentar ala familia
2 PEDRO: era un hombre cuyo trabajo era la pezca y iba a los mercados y los vendía y de hay se sustentaba
3 PABLO: era un hombre cuyo trabajo o empreza era hacer tiendas de campaña para ganar dinero
4 JACOB: era un hombre cuyo trabajo era cultivar maíz, cuidar ganados para poder ganar dinero y así se volvió rico
5 JOSE HIJO DE JACOB: era el administrador de Egipto en toda la parte económica como los ganados, cultivos, de todo Egipto
martes, 16 de febrero de 2016
FUNCIONES LINEALES DE COSTOS
El costo es la expresión cuantitativa monetaria representativa del consumo necesario de factores de la producción que se emplean para producir un bien o prestar un servicio.
Con las funciones de costos trataremos de plantear un modelo matemático simplificado de la realidad económica. Iniciaremos diciendo que los costos de producción de un bien o de prestación de un servicio tienen distintos componentes que, en un principio, le atribuiremos un comportamiento lineal, pues es el modelo más sencillo.
Las funciones lineales cumplen un importante papel en el análisis cuantitativo de los problemas económicos. En muchos casos los problemas son lineales pero, en otros, se buscan hipótesis que permitan transformarlos en problemas lineales ya que su solución es más sencilla.
Costo lineal
Cuando una empresa produce cualquier bien o presta un servicio, deberá utilizar una serie de insumos que valorizados monetariamente le genera costos, que analizados en función a la relación con la producción total, los denominaremos costos fijos y costos variables. Los primeros, como lo indica su nombre, son independientes de las cantidades de un artículo que se produzca o un servicio que se preste (p.ej.: alquiler del local, depreciación de los bienes durables, determinados impuestos, etc.). En cambio, los costos variables dependen de la cantidad que se produzca de ese artículo o que se preste del servicio, (p. ej.: costos de materiales, de mano de obra productiva, etc.)
Ejemplo 1 : El costo variable de fabricar juntas para machimbre es de $ 2 por unidad y los costos fijos por día son de $30. Escriba la fórmula de costo total y construya su gráfica
¿Cuánto cuesta fabricar 25 juntas de machimbre por día?
Solución :
El costo total de fabricar x juntas de machimbre en un día es
C(x) = 2x + 30
El costo total de fabricar 25 juntas de machimbre por día es de $ 80.
C(25) = 2. 25 +30
C(25) = 80
Ejemplo 2: El costo de fabricar 10 bolsas de cartón al día es de $2,20, mientras que fabricar 20 bolsas del mismo tipo cuesta $ 3,80. Suponiendo que se trate de un modelo de costo lineal, determine la fórmula correspondiente a producir x bolsitas de papel en el día y construya su gráfica.
Solución:
En este caso tenemos dos puntos P(10; 2,2) y Q (20; 3,80), pudiendo construir la ecuación que determine la relación.
y = 0,16x+0,6
En el gráfico observamos que como x puede tomar únicamente valores enteros no negativos, no podemos representar a la función como una linea recta continua.
Generalmente, cuando se trabaja con funciones económicas, se considera el dominio real, por lo que se la representa como una línea continua.
Suscribirse a:
Entradas (Atom)


